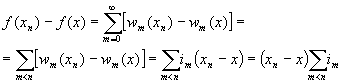Blancmange function in [0,1]

Blancmange function

is nowhere differentiable in [0,1]

Proof:

Blancmange function is the sum of the series :

Let x be a point in [0,1].

For each natural n, select x_n in [0, 1] such that either:

or

, chosen such that the interval between x and x_n lies, for some k<2ⁿ, entirely inside [k2^n-1, (k+1)2^n-1]. Clearly, x_nà x.

The terms w_n(x) are periodic with period 2^-m, and for m>n , 2^-n is multiple of

2^-m. So for m≥n:

For m<n, since the terms w_n(x) are linear with slope 1 or –1 on the segment between x and x_n, we have:

As a consequence, for each n:

where i_m are all 1 or –1.

Since all x_n ≠x, either {x_n}_n has a subsequence with terms less then x, or {x_n}_n has a subsequence with terms more then x. Lets consider the first case, e.g. {x_n}_n has a subsequence with terms less then x, and let’s call that sequence {y_n}_n. In general,

, where {k_n}_n is an increasing sequence of natural numbers.

Let’s consider {D_n}_n , where

.

From previous calculations:

Considering that (i_m)_m<n are calculated for each n, we should have written (i_m,n)_m<n instead of (i_m)_m<n. However, i_m,n1=i_m,n2 for m<min(n1,n2), since [y₁,x] contains all [y_n,x] and all series terms are linear on [y1, x].

So, for each n, either D_n+1=D_n+1 or D_n+1=D_n-1. As a consequence, D_n is not convergent.

If Blancmange would be differentiable at x, then D_nàf’(x), but we proved that D_n is not convergent. As a consequence, the function is not differentiable at x █